Statistica descrittiva

Andiamo a descrivere una popolazione tramite un campione che assumiamo essere rappresentativo della popolazione, diciamo che N è la dimensione del campione dove N è il numero di osservazioni di cui è costituito il campione.

Frequenza assoluta:

 La frequenza assoluta di un osservazione w è il numero di volte che si è osservata nel campione e la indicheremo con N(w).

Frequenza relativa:

 La frequenza relativa di un osservazione w è il rapporto tra tra il numero di volte che si osserva w nel campione [N(w)] e la dimensione del campione [N].

Possiamo rappresentare la frequenza relativa e assoluta tramite dei grafici.

Esempio: lancio di un dado 24 volte

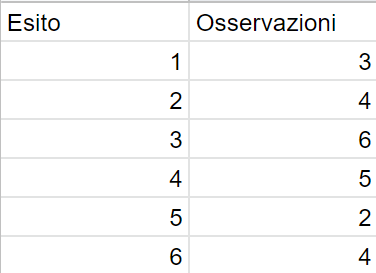
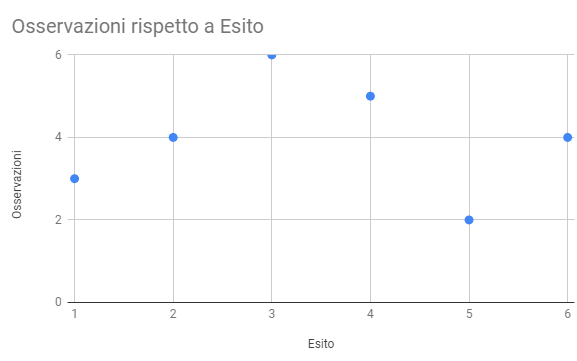
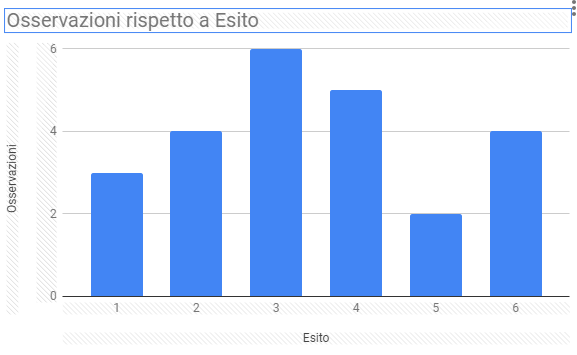
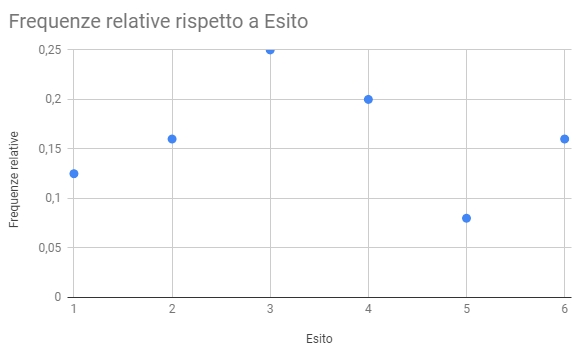
Frequenza cumulativa

 E' l'equivalente della funzione di distribuzione 

Percentili

Si dice n-essimo percentile l'osservazione w per cui F(w)=n/100 più in generale se viene chiesto l'n-esimo quartile ad esempio prenderemo w per cui F(w)= n/4 e cosi via in base alla frazione che viene richiesta. Da questo punto di vista possiamo definire la mediana come il 50-esimo percentile. La moda anche nella statistica descrittiva viene intesa come il valore più frequente. Per la media parleremo di media aritmetica e ponderata, la media aritmetica è la sommatoria dei valori osservati fratto il numero di campioni mentre la media ponderata vede i campioni pesati con dei coefficienti e poi la sommatoria suddivisa per la somma dei coefficienti.

Scarto assoluto medio 

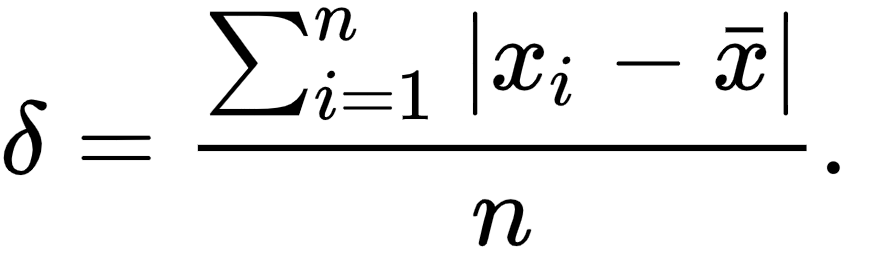
E' una misura della dispersione in una popolazione, da non confondere con la varianza che viene detta invece scarto quadratico medio e si ottiene dividendo per n-1 e non per n.

Variabili aleatorie vettoriali

Ci si introduce facilmente considerando che tutte le integrazioni fatte andranno trasformate in integrali doppi, tripli, n-pli in base alla dimensione della variabile aleatoria. Introdurremo invece il nuovo concetto di distribuzione marginale, covarianza e di densità di probabilità condizionata.

Distribuzioni marginali:

Immaginate questa distribuzione di due variabili

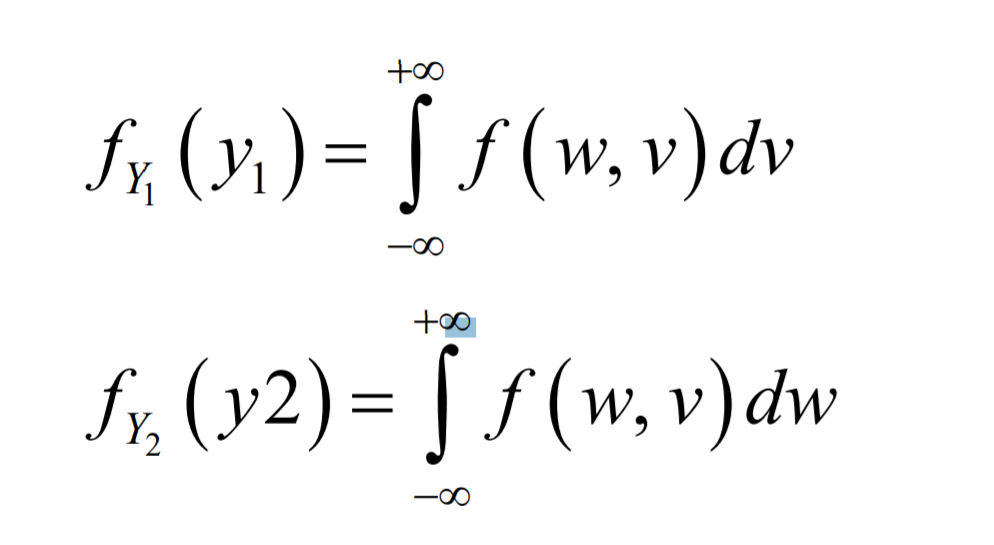
Fissando y1 e integrando rispetto a y2 si ottiene la distribuzione marginale di y2 per quel valore di y1 e viceversa.

Covarianza;

 E'la media dei prodotti delle distanze dalla media dei valori di ciascuna variabile

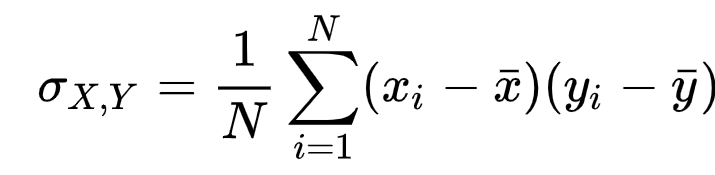
Indice di correlazione 

E' un indice che ci da informazioni sul fatto che vi sia una relazione lineare tra le due variabili.

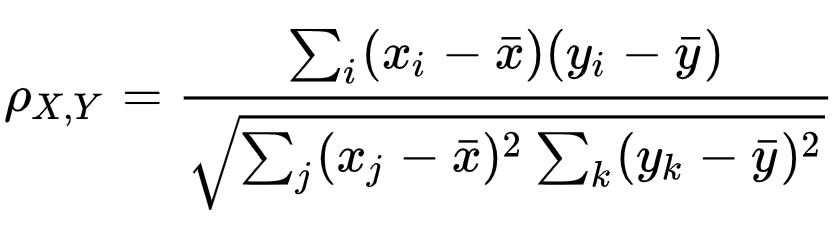
Densità di probabilità condizionata:

 La otteniamo muovendoci su una riga o su una colonna della matrice all'inizio