Multiplexer

Multiplexer

Il multiplexer è un circuito combinatorio caratterizzato con 2^n linee di ingresso ed n bit di controllo, detti anche linee di selezione o ingressi di indirizzo. Ogni combinazione delle linee di selezione invierà in uscita il bit di ingresso Ik dove k è la combinazione descritta dalle linee di selezione.Analizziamo ora il più semplice multiplexer (quello con due ingressi da un bit e un uscita) compilando la tabella di verità per poi ricavarne la mappe di Karnaugh.

Dalla mappa di Karnaugh viene fuori U=I0S'+I1S

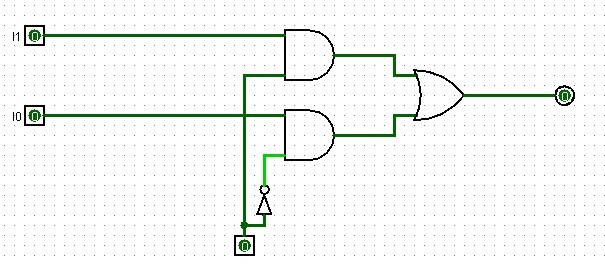
Se volessimo lavorare con m ingressi ci servirà un multiplexer con 2^n ingressi, dove n è il minor numero naturale per cui 2^n>=m. Vale a dire che se ho 5 ingressi userò un multiplexer con 8 ingressi e tre linee di selezione in quanto 2^2=4<5, 2^3=8>5 dunque un multiplexer con 2 linee di selezione non è sufficiente per selezionare tra 5 ingressi e il minor n per cui è verificata la relazione è n=3. Vediamo ora l'esempio con 4 ingressi che avrà di conseguenza 2 linee di selezione.

In questa tabella di verità ridotta ogni riga i rappresenta una situazione in cui tutti gli ingressi Im per cui m è diverso da i siano variabili "don't care". Otteniamo la funzione booleana U=I0S1'S0' + I1S1'S0 + I2S1SO' + I3S1S0

Ricavare l'espressione booleana di un multiplexer

Ora numeriamo ogni porta AND con k e definiamo una funzione booleana che descriva il funzionamento di qualsiasi multiplexer con 2^n ingressi. Consideriamo k appartenente a [0,2^n -1], x=(x0,x1,...,xn), y=(y0,y1,...,yn) e definiamo la relazione mk:{0,1}^n ---> {0,1}^n x--->y dove -mk(x)=1 se e solo se la sommatoria da 0 a n del prodotto xi(2^i) è uguale a k -mk(x)=x altrimenti.ovvero abbiamo -yi=xi' se xi=0 e k=sommatoria da 0 a n di xi(2^i) -yi=xi altrimenti.Ora poniamo mk(x)= y1 AND y2 AND...yn.Detto ciò possiamo definire l'uscita di un generico multiplexer come la sommatoria da 0 a 2^n-1 di mkIkEssendo mk il risultato dell'AND tra tutti i bit di mk basta inviare in ingresso alla porta AND k-esima tutti i bit di mk assieme all'ingresso Ik per realizzare la funzione mkIk, dopo di che effettuando l' OR tra tutti i risultati di mkIk (per ogni k da 0 a 2^n -1) otteniamo fisicamente la sommatoria che abbiamo usato per descrivere l'uscita del MUX.

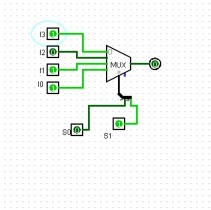
Considero compreso il funzionamento del multiplexer pertanto d'ora in poi rappresenteremo i MUX con il simbolo nell'immagine qua sotto.

Il multiplexer può essere usato come generatore di funzioni. Prendiamo la tabella di verità di una rete combinatoria a caso per fare un esempio.

Ora per "generare" la funzione ci basterà usare un MUX con n=2 bit di selezione (dove n è il numero di bit in ingresso alla rete combinatoria descritta nella tabella di verità) e fissare il valore di 2^n=4 bit in ingresso al multiplexer. L'i-esimo bit dovrà assumere il valore che l'uscita assume nell'i-esima combinazione degli ingressi. Nel caso dell'esempio precedente abbiamo fissato I0=1 I1=1 I2=0 I3=1 in ingresso al multiplexer. Se abbiamo situazioni dove l'uscita è d basterà non collegare niente nel corrispondente ingresso del multiplexer (se ricordate d sta per don't care)

Algoritmo:

1. Si usa un mux con tante linee in ingresso quante sono le righe della tabella di verità da realizzare

2.Si impone il valore degli ingressi seguendo le indicazioni sulla colonna dell'uscita nella tabella di verità

3.si collegano le variabili in ingresso della tabella di verità come linee di selezione del multiplexer.

Multiplexer con dati composti da più di un bit

Chiamiamo A1 e A0 i bit che compongono il dato A e B1, B0 i bit che compongono il dato B.

Vogliamo avere in uscita i due bit di A quando il selettore vale 0 e quelli di B quando il selettore vale 1. Lo stesso ragionamento potrà essere applicato anche a dati di più bit utilizzando dando in ingresso l'n-esimo bit di ogni dato all'n-esimo multiplexer.

Vediamo l'esempio su logisim

essere abbastanza per tutti i dati in ingresso dunque usiamo multiplexer con 2^n ingressi dove n è il più piccolo numero naturale per cui 2^n è maggiore o uguale al numero di dati in ingresso. Per esempio per 5 dati a 3 bit userò 3 multiplexer con 8 ingressi, per 4 dati da 1 bit un multiplexer a 4 ingressi e cosi via.

2. Collego le stesse linee di selezione a ogni multiplexer.

Chiarimento riguardo all'uso delle porte AND nei multiplexer

Come Abbiamo ripetuto infinite volte, la porta AND ha in uscita 1 solo se tutti i suoi ingressi valgono 1, per tanto se con n ingressi imponiamo il valore di n-1 ingressi come 1 allora la porta AND avrà in uscita il valore del restante bit in ingresso in quanto se quel bit vale 1 allora tutti i bit valgono 1 e se quel bit vale 0 implica uscita nulla.

Come facciamo a scegliere se inviare in uscita il dato oppure no?

Prendiamo la singola porta AND a cui è collegato l'ingresso I0 di un multiplexer a 4 ingressi e un uscita. Noi vogliamo che in uscita si abbia l'ingresso I0 in corrispondenza dei valori 00 dei bit di selezione, per il funzionamento della porta AND si avrà I0 in uscita solo quando tutti i bit di selezione valgono 1 quindi nel caso di I0 negheremo tutti i bit di selezione prima di farli entrare nella porta AND.

Nel caso della porta AND collegata all'ingresso I1 vogliamo in uscita I1 quanto i bit di selezione valgono 01 per tanto negheremo solo S1 in ingresso alla porta in modo da ottenere 11 in ingresso alla porta AND.

Ripetendo ricorsivamente questo procedimento arriviamo allo schema presentato precedentemente per il multiplexer 4-1.

Il procedimento appena descritto è l'implementazione fisica della funzione mk descritta nel paragrafo "Ricavare la funzione booleana di un multiplexer" in cui usavamo la definizione di mk per sapere quali bit negare per ogni porta AND.