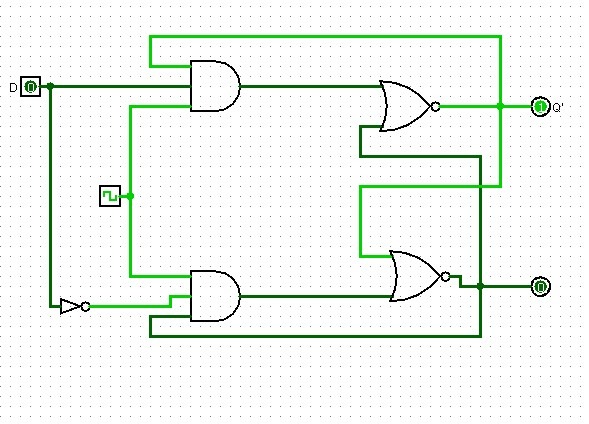
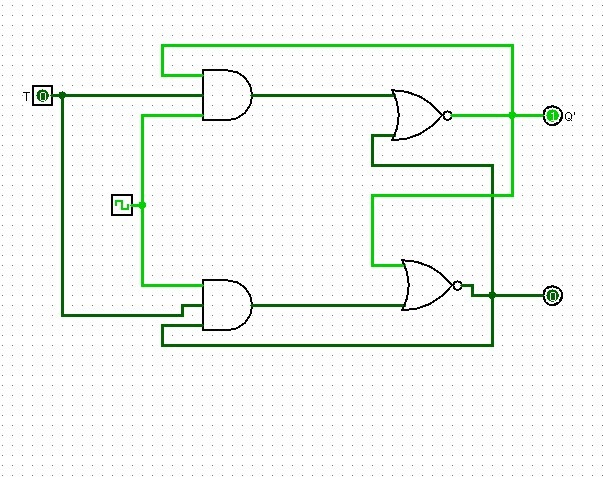
Latch

Latch set-reset

Per comprendere il Latch non proveremo a ragionare su come ottenerlo ma partiremo dal Latch e analizzandolo ne studieremo il funzionamento.

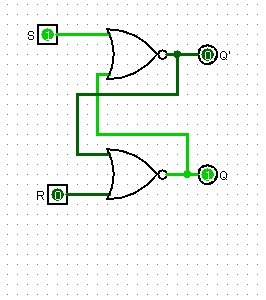
Ora abbiamo Q(t+1)=(Q'(t)+R)'=((S+Q(t))'+R)'=(S+Q(t))R'
Tramite questa formula possiamo compilare la tabella di verità del Latch

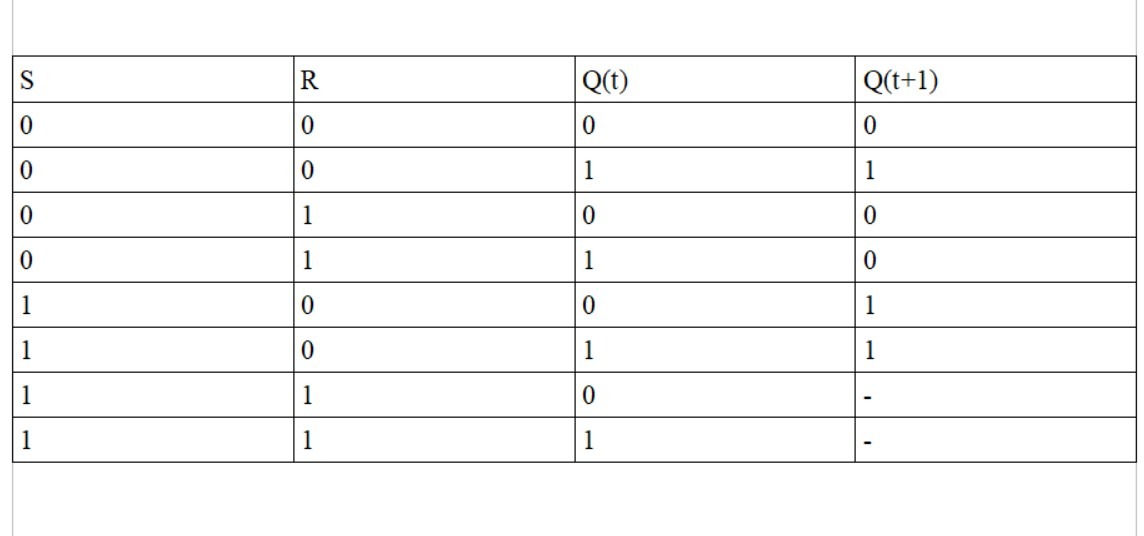
Tabella di verità Latch set-reset

Come notiamo dalla tabella di verità, ogni volta che S=1 e R=0 l'uscita Q(t+1)=1, Se R=1 e S=0 abbiamo Q(t+1) =0 mentre se S=R=0 abbiamo Q(t+1)=Q(t). Nel caso in cui S=1 e R= 1 lo strumento non funziona correttamente in quanto risulta Q(t)=Q'(t), il che rende indeterminato lo stato successivo.

Purtroppo se volessimo far cambiare contemporaneamente lo stato di S e R da 0 a 1 la retroazione delle uscite del Latch raggiungerebbe l'ingresso delle porte NOR troppo lentamente e il dispositivo incorrerebbe in un oscillazione delle uscite Q e Q' a causa del susseguirsi di aggiornamenti continui in ingresso alle porte NOR. Basti pensare che ogni porta NOR ha in ingresso l'uscita dell'altra porta NOR e se portiamo lo stesso dato in ingresso ad entrambe le porte, al variare del dato, le porte riceveranno un ingresso contemporaneamente e contemporaneamente genereranno l'uscita, il problema è che dipendendo una dall'uscita dell'altra, per poter funzionare, ogni porta ha bisogno che l'uscita dell'altra porta sia stabile in ingresso ad essa. Facciamo un esempio con logisim.

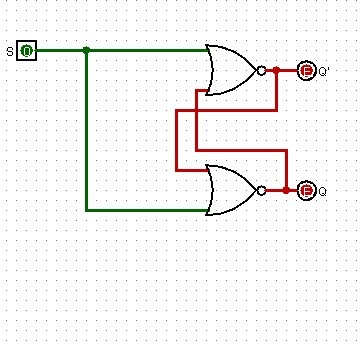
Per ora S=R= 0 e sia Q' che Q sono ancora nulli, proviamo ad azionare il Latch S-R per la prima volta ponendo S=R=1

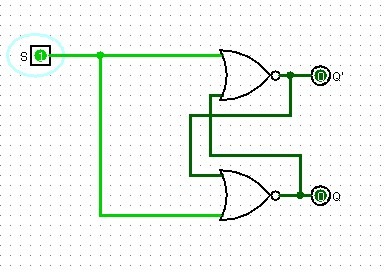
Configurazione non ammessa

Ora S valeva 1 e sia Q che che Q' erano stabili con valore nullo in ingresso alla porta NOR dunque tutto è andato liscio e siamo entrati nella configurazione non ammessa. Ora facendo tornare S=R=0 ci aspettiamo Q(t+1)=Q(t) come risulta nella tabella di verità ma una volta aggiornati Q(t+1) e Q(t+1)' rientreranno in ingresso alle porte NOR pur se non cambiamo il valore di S. Nella porta NOR Q(t) viene sommato con 0 (in quanto S=R=0) e poi viene negato dunque di volta in volta il segnale Q(t) entrerà nella porta NOR e verrà semplicemente negato. Il risultato e che passando S=R=1 a S=R=0 siamo entrati in una situazione dove le uscite vengono negate di continuo variando da 0 a 1 e viceversa per causa della retroazione.

Chiaramente in quanto in tutte le altre configurazioni Q!=Q' non incorriamo nel fenomeno dell'oscillazione, seppur cambiamo contemporaneamente il valore di S e R in quanto non essendo ammessa la configurazione 11 il fatto che uno sia alto implica che l'altro sia basso, otteniamo nel caso S=1 R=0 che Q sarà sempre il NOR tra Q' e 0, ovvero Q=(Q')'=Q il che significa che Q resterà comunque stabile a fronte di cambiamenti contemporanei da S=0 e R=1 ai loro valori negati. Nel caso inverso si dimostra in maniera analoga la stabilità degli ingressi, se consideriamo che per passare a uno stato degli ingressi dobbiamo necessariamente essere in un altro stato e consideriamo il valore di Q(t) in quello stato notiamo che viene sempre rispettata la tabella di verità. Nel caso 00 Abbiamo Q'=QNOR0=Q' e Q=Q'NOR0=Q dunque sappiamo sia che il dato resterà stabile sia che viene rispettata la tabella di verità.

Abbiamo caratterizzato tutti i casi del Latch esclusi quelli in cui dalla configurazione degli ingressi 11 si passa a 10 o a 01, anticipo che chiaramente lo stato 11 causerà indeterminazione dello stato successivo con conseguente oscillazione delle uscite a seguito della variazione di S o R ma lascio al voi il ragionamento a riguardo e la spiegazione.

La maggior parte dei testi da per verità assoluta che la configurazione 11 sia non ammessa ma non argomenta ciò che succede. Non avendo raccolto le informazioni, riguardo lo stato 11, da dei libri ma avendole ricavate tramite simulazioni e ragionamento invito qualsiasi lettore a rendermi presenti possibili inesattezze (anche se dubito che sia possibile trovare degli errori in quanto ogni singolo passo del ragionamento è stato simulato al calcolatore).

Latch S-R sincrono

Il primo dispositivo sincrono che vedremo sarà il Latch S R sincrono, ottenuto sostituendo S con SANDclock e R con RANDclock, in modo da tenere nulli gli ingressi al latch quando il clock vale 0.

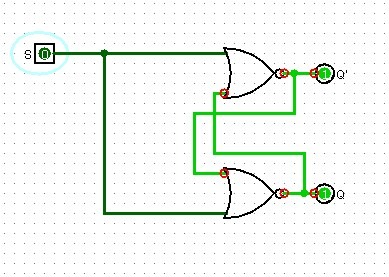
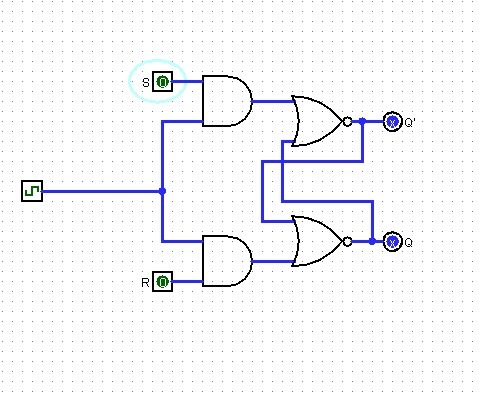
In questo caso le uscite cambiano solo durante gli intervalli di tempo in cui il clock è alto, la configurazione 1 1 è ancora proibita (genera un oscillazione delle uscite) infatti impostando 11 con il clock basso

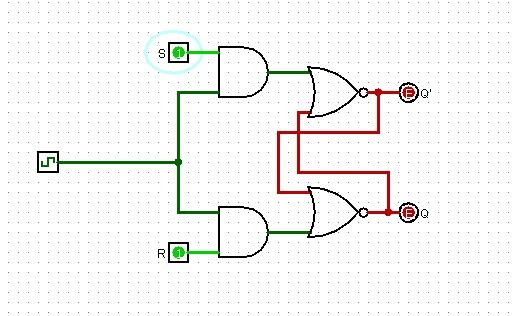
e alzando il clock entriamo nella configurazione non ammessa in cui come abbiamo detto Q'=Q.

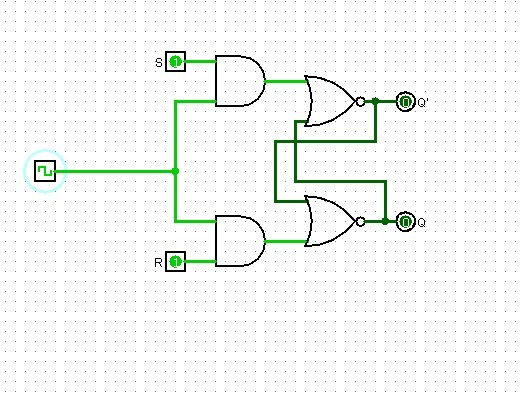
Configurazione non ammessa

La configurazione non ammessa è tale in quanto la situazione Q=Q' causa l'indeterminazione dello stato successivo infatti al prossimo colpo di clock noteremo l'effetto con l'oscillazione delle uscite

Dunque l'unica differenza tra il Latch S-R sincrono e asincrono sta nel fatto che in uno le uscite variano con continuità e nell'altro solo quando il clock è alto.

Quando il clock è basso il Latch S-R sincrono è nella configurazione 00 dunque siamo sicuri che le uscite mantengano il loro valore per tutto il periodo basso del clock.

Latch JK

Il Latch jk si differenzia dal SR in quanto nel caso del jk la retroazione arriva anche alle porte AND e non solo alle porte NOR. In questo modo ci si libera del problema della configurazione non permessa e l'uscita futura dipenderà da quella attuale e da J se Q(t)=0 o K se Q(t)=1, in entrambi i casi se J o K=1 l'uscita si inverte mentre si mantiene con uno 0 in ingresso.

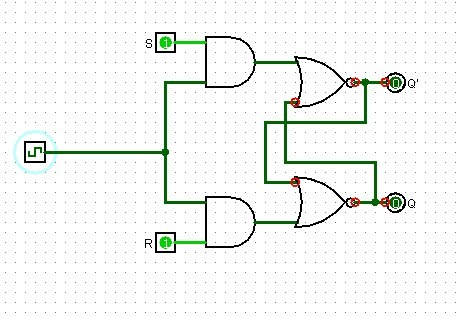
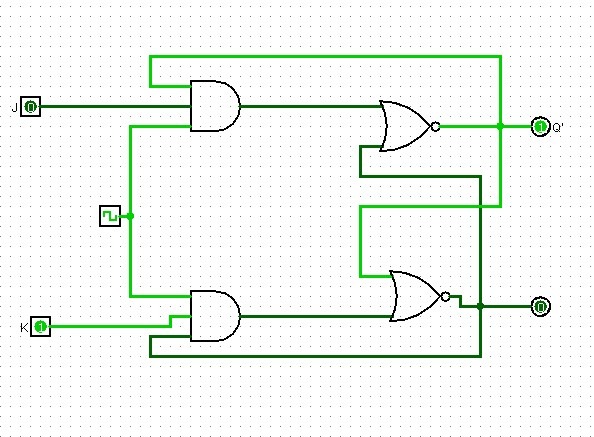
Latch D e T
Vengono ottenuti entrambi a partire dal JK collegando gli ingressi,
-nel caso del Latch D l'ingresso è D=J=K' dunque lo stesso ingresso viene mandato sia a J che a K ma viene negato in K,
-nel caso del Latch T abbiamo T=J=K quindi semplicemente lo stesso ingresso viene collegato sia a J che a K
Vediamo qui sotto gli schemi e le tabelle di verità